Razon y proporcion

Unidad: 
 Conjunto de los numeros racionales
Contenido:
Razon y proporcion

 Magnitud:

    Una magnitud física es una propiedad o cualidad medible de un sistema físico, es decir, a la que se le pueden asignar distintos valores como resultado de una medición o una relación de medidas. Las magnitudes físicas se miden usando un patrón que tenga bien definida esa magnitud, y tomando como unidad la cantidad de esa propiedad que posea el objeto patrón. Por ejemplo, se considera que el patrón principal de longitud es el metro en el Sistema Internacional de Unidades.
Existen magnitudes básicas y derivadas, y constituyen ejemplos de magnitudes físicas: la masa, la longitud, el tiempo, la carga eléctrica, la densidad, la temperatura, la velocidad, la aceleración y la energía. En términos generales, es toda propiedad de los cuerpos o sistemas que puede ser medida. De lo dicho se desprende la importancia fundamental del instrumento de medición en la definición de la magnitud.

Entonces una magnitud es cualquier propiedad que se puede medir numericamente.

Razon:

 En matemáticas la razón es una relación binaria entre magnitudes (es decir, objetos, personas, estudiantes, cucharadas, unidades del SI, etc.), generalmente se expresa como "a es a b" o a:b. En el caso de números toda razón se puede expresar como una fracción y eventualmente como un decimal

  

 

 Una razon se puede exprear como:

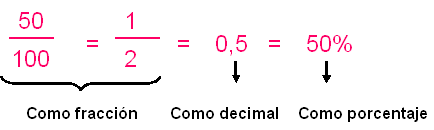
Proporcion:

Una proporción es una igualdad  entre dos razones , y aparece frecuentemente en notación fraccionaria.
Por ejemplo:
 
 2   =  6
 5      15
 Para resolver una proporción, debemos multiplicar cruzado para formar una ecuación.

Ejemplo:
 
2   = 8
x     16
 
Ahora, se multiplica cruzado.
2 · 16  =  8 · x
32 = 8x                     Se resuelve la ecuación.
32  =  8x
 8       8
4 = x                          El valor que hace cierta la proporción es 4 es decir:
 
                       2 = 8
                        4   16

Aplicación:

Para hacer sorullitos, mi vecina usa: 3 tazas de harina de maíz por 1 taza de líquido ( que contiene agua, azúcar, sal y mantequilla). Si ella quiere hacer 13 tazas de harina, ¿cuánto líquido debe agregarle?
Hagamos una proporción:
                                   harina   =   harina
                                    líquido        líquido
 
                       3 tazas harina   =    13 tazas
                        1 taza líquido          x tazas líquido
 
     x es el valor que busco; en este caso, es el líquido para las 13 tazas de harina.
                           3     =     13
                            1             x
Ahora, se multiplica cruzado.
                            3 · x  =  13 · 1
                            3x = 13
Se resuelve la ecuación para encontrar el valor de x.
                           3x  =   13
                            3          3
                                x =  4.3
La x  es igual a 4.3 . Por lo tanto, para 13 tazas de harina, se necesitan 4.3 tazas de líquido para poder hacer los sorullitos.
Otra aplicación:
 
Mi vecina ahora quiere hacer sorullitos, y ya sabemos que ella utiliza 3 tazas de harina por 1 taza de líquido. Ella ya tiene preparado 5.5 tazas de líquido. ¿Cuántas tazas de harina necesita para hacer los sorullitos?
 
                   harina   =   harina
                    líquido       líquido
 
                3 tazas harina    =      x  tazas harina
                  1 taza líquido            5.5 tazas líquido
 
                                     3  =   x
                                      1      5.5
                                    3 · 5.5  = x · 1
                                    16.5 = x
 
Quiere decir, que para 5.5 tazas de líquido se necesitan 16.5 tazas de harina.
 
 
Proporciones utilizando por ciento
 
 %  =   porción de un número
100         total del número
 
 

¿ Cuál es el 12% de 658?    12    =   X   100      658    12 ·  658 = 100 ·X    7896 = 100 · X   7896 = 100X    100      100   78.96 = X

Estamos buscando una porción de 658 . En esta proporción, hay que ver que 12/100 está dado por 12%. Al otro lado de la proporción, va la proporción y  porción/total. No sabemos la porción, así que la x va arriba. Abajo va el total, que es 658.

 

¿ Cual es el 30% de 84? 30  =  X 100   84 30 · 84 = 100 · X 2520 = 100X 2520 = 100X  100      100 25.2 = X	Sabemos que el 30% se expresa  30/100.  Como estamos buscando la porción de 84, la X va arriba como numerador; y el total, que es 84, va abajo como denominador.
¿ El 3% de que número es 5.4?   3  = 5.4 100     X 3 · X = 5.4 · 100 3X =  540 3X  = 540  3         3 X = 180	Tenemos el 3% dado por 3/100. Vemos que 5.4 es una porción de un número que no sabemos.  Así que se está buscando el total. Por eso, la x va abajo, en el denominador.

 
 
 

¿ 85 es qué % de 180?  X  =  85 100     180   X · 180 =  85 · 100 180X = 8500 180X  = 8500  180        180 X  = 47.2

No tenemos el porciento;  y la porción es 85 y el total es 180. Así que la x va en la parte izquierda de proporción, arriba.

  Problemas de Aplicación:
A. Durante  25 minutos de ver televisión, hay 7 minutos de anuncios comerciales. Si ves 70 minutos de televisión, ¿cuántos minutos de anuncios verás?
 
 
                   25 minutos T.V.   =    70 minutos T. V.
                      7 min. anuncios       x  min. anuncios
                                   25    =     70
                                     7             x
                                 25 · x  =  70 · 7
                                 25x = 490       (Resolver Ecuación)
                               25x =  490
                                25        25
                                x = 19.6
Por lo tanto,  en 70 minutos de ver televisión , hay 19.6 minutos de anuncios comerciales.
 
B.  Si una docena de huevos  cuesta $1.50, ¿cuál será el costo de   100 huevos?
               docena huevos   =     100 huevos
                        1.50                            x
 
                       12     =      100
                       1.50               x
                        12 · x = 100 · 1.50
                        12x = 150          (Resolver Ecuación)
                       12x   =   150
                        12           12
                          x  =  12.5
Por lo tanto, si una docena de huevos cuesta $1.50, 100 huevos cuesta $12.50. 
Ejercicios
 
Encontrar el número que falta utilizando proporciones.
a)    3  =   1
        x        2
b)    2  =   x
        9       18
c)    x   =    6
       4         8
d)    2   =   4
       9         x
 
Problemas de Aplicación:
1)  Juan piensa hacer un bizcocho  para una fiesta.  Para ello, utiliza 1 taza de agua por 3 tazas de mezcla.  El paquete  contiene 14.5 tazas. ¿ Cuántas tazas de agua debería usar?
2)  Si una docena  de empanadillas cuesta $ 6.00 en la compañía  Kikuet, cuánto costará 500 empanadillas?
3)  Durante 60 minutos de escuchar la radio ,12.5 minutos son anuncios.  Si escuchas la radio por 6 horas y 15 minutos , cuántos minutos escuchaste de anuncios?
Proporciones utilizando porciento:
1)  ¿ Cuál es el 15% de 60?
2)  ¿ 30% de qué es 40%?
3)  25 es qué porciento de 90?