Regla de tres simple directa e inversa

Unidad:
Proporciones
Contenido:
Regla de tres simple directa e inversa.

Regla de tres

La regla de tres es una operación que tiene por objeto hallar el cuarto término de una proporción, cuando se conocen tres (Ver tema “razones y proporciones” y Variación directa y variación inversa” en este sitio).

Supuesto y pregunta

En una regla de tres hay dos partes: el supuesto que está constituido por los datos de la parte del problema que ya se conoce y la pregunta que la constituyen los datos de la parte del problema que contiene la incógnita.
Ejemplo.
PROBLEMA 1.
Si 14 lápices cuestan $42.00, ¿cuánto costarán 25 lápices? SUPUESTO: 14 lápices… $42.00, PREGUNTA: 25 lápices… X pesos
Ejemplo.
PROBLEMA 2.
Si 5 obreros hacen una obra en 40 días, ¿cuánto tardarán 8 obreros en hacer la misma obra? SUPUESTO: 5 obreros…40 días PREGUNTA: 8 obreros… X días
Ejemplo.

MÉTODO PRÁCTICO
Primero hay que identificar las magnitudes que intervienen en la situación y qué tipo de regla de tres es.
A las magnitudes que sean directamente proporcionales con la incógnita se les pone debajo un signo más (+) y encima un signo menos (–), a las magnitudes que sean inversamente proporcionales con la incógnita se le pone debajo un signo menos (–) y encima un signo más (+) y el valor de la incógnita x será igual al valor conocido de su misma especie y siempre se le pone el signo más (+). Resolvamos los mismos ejemplos.
PROBLEMA 1.

Se escriben el supuesto y la pregunta.

Se compara cada una de las magnitudes de la pregunta con la incógnita para ver si son directa o inversamente proporcional con la incógnita.
Comparamos: A mayor número de lápices (25), mayor será el precio (mayor que $42.00). Entonces estas magnitudes son directamente proporcionales; se pone el signo más (+) debajo de los 25 lápices y el signo menos (-) encima de 14 lápices. Encima de $42.00 se pone el signo más (+)

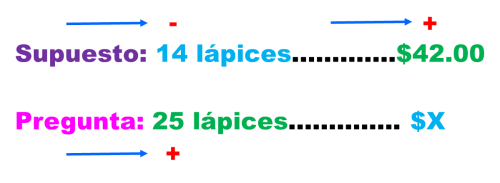
Hecho esto, se multiplican las cantidades que llevan el signo más (+) y se divide entre la cantidad que lleva el signo menos (–) para obtener la respuesta del problema.

Por lo tanto, por 25 lápices costarán $75.00

PROBLEMA 2.

Se escriben el supuesto y la pregunta.

Se compara cada una de las magnitudes con la incógnita para ver si son directa o inversamente proporcional con la incógnita.
Comparamos: A mayor número de obreros (8), menor será la cantidad de días (menor que 40). Entonces estas magnitudes son inversamente proporcionales; se pone el signo menos (-) abajo de 8 obreros y arriba de los 5 obreros se pone más (+). Arriba de 40 días se pone más (+).

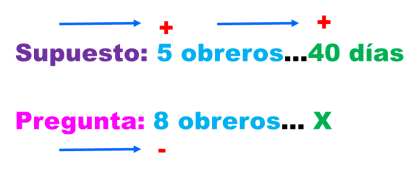
Hecho esto, se multiplican las cantidades que llevan el signo más (+) y se divide entre la cantidad que lleva el signo menos (–) para obtener la respuesta del problema.



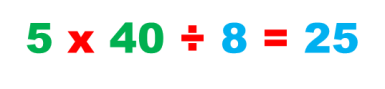
Resuelve los siguientes problemas aplicando lo que has aprendido sobre regla de tres simple directa e inversa.
Recuerda que la sala telematica es para trabajar y realizar las actividades que se te piden. MUCHAS GRACIAS.

1. Dos ruedas están unidas por una correa transmisora. La primera tiene un radio de 25 cm y la segunda de 75 cm. Cuando la primera ha dado 300 vueltas, ¿cuántas vueltas habrá dado la segunda?

2. Seis personas pueden vivir en un hotel durante 12 días por 7920 cordobas. ¿Cuánto costará el hotel de 15 personas durante ocho días?

3. A las 6:00 un reloj recibe un golpe y debido a ello empieza a atrasarse 6 minutos cada hora.
¿Qué hora marcará el reloj cuando sea la mima hora, pero del día siguiente?
A) 0:36         B) 1:36             C) 2:36             D) 3:36               E) 4:36

 4. El sacristán de una iglesia, da 6 campanadas en 8 segundos. ¿Cuántas campanadas dará en 24
segundos?
A) 24            B) 20              C) 16          D) 12            E) 6

5.  Una oveja atada a un poste con una soga de 4m, demora 8 horas en comer el pasto a su alcance.
¿Cuánto demoraría en comer el pasto a su alcance, si la soga midiese 2m?
A) 3 horas            B) 4 horas            C) 2 horas          D) 1,5 horas          E) 2,5 horas

6.  Un grifo atascado gotea 0,042 litros cada minuto. ¿Cuántos litros de agua se perderán en un día?
A) 60,48        B) 1,008        C) 42,00        D) 151,20 

7. Para la preparación de una mermelada se necesitan 12 manzanas que cuestan en total $1.60. ¿Cuánto costarán 72 manzanas?
A) $9.0            B) $9.4             C) $9.6          D) $9.8  

8. Si un campanario toca 10 campanadas en 27 segundos. ¿Cuántas campanadas tocará en un minuto?

A) 20

B) 18

C) 22

D) 21

E) N.A.

9. Si la distancia entre la Tierra y el Sol es 150 millones de kilómetros, ¿Cuántos años tardaría en llegar al sol un cohete que viaja a 2000 km/h?
A) Entre 4 y 6 años                  B) Entre 6 y 8 años          
C) Entre 8 y 10 años                D) Entre 10 y 12 años

10. Una fotocopiadora saca un millar de hojas oficio en 7 minutos. ¿Cuántas horas demora en sacar 20  millares de hojas oficio?
A) 2  1/3        B) 1 1/2        C) 1  1/4        D) 3  1/2      E) N.A. 

11. En un cuartel 200 soldados tienen comida para 40 días, si se cuadriplicara el número de soldados. ¿Cuánto tiempo les duraría la comida?
A) 12 días        B) 14 días          C) 10 días        D) 20 días         E) 16 días  

12. Una obra puede ser realizada por 6 obreros en 20 días. ¿Cuántos obreros más se necesitarán para hacer  el mismo trabajo en las 3/10 partes de ese tiempo?
A) 10             B) 20             C) 14            D) 5            E) 1

13. Un grupo de cinco cocineros iban a preparar un banquete en 6 horas. ¿Qué tiempo demoran 3 cocineros en preparar dicho banquete?
A) 8 h        B) 9 h        C) 10 h       D) 12 h     E) 14 h   

14. Entre dos personas pintan una casa en 36 horas, si dicha labor la llevaran a cabo 3 personas, ¿cuánto tiempo demorarán en pintar la casa?

15. A la fiesta asistieron 10 personas y cada una de ellos les tocó 1/10 del pastel. Si 8 personas asistieron a la fiesta, ¿qué parte del pastel le tocaría a cada uno?